目录
基本概念
事件(event)
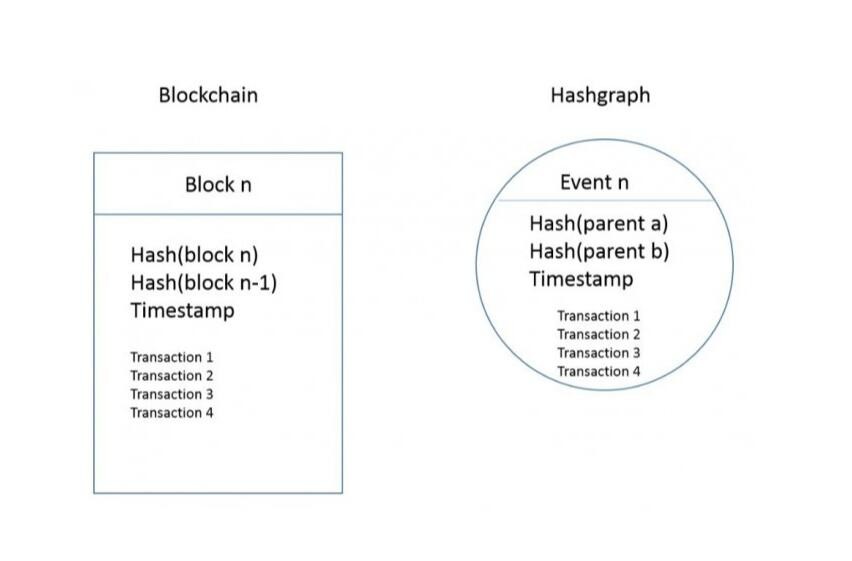
类似于一般区块链中的区块,事件是一个包含有两个哈希指针的数据结构,并且可以包括0个或若干交易信息,节点在创建事件的同时会加上时间戳并且对整个事件数字签名;
绝对多数(supermajority)
超过2/3以上节点的数量,在很多DPOS系算法上也有这个概念;
可见(seeing)
当事件B可以沿着哈希指针找到事件A,那么事件B就可见事件A;
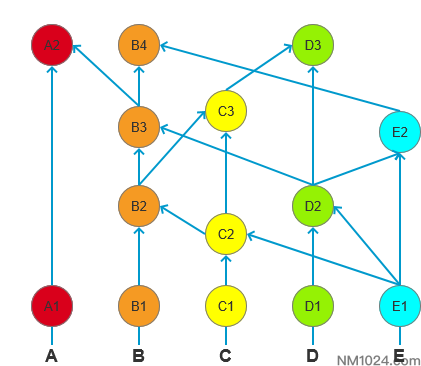
下图中每个圆形表示一个事件,共有ABCDE5个节点,则其绝对多数为5*2/3,箭头表示将当前事件发送到某个节点,构成一个新的事件(下同)。
图中A2可见B1,因为A2是由A1+B3组成,从A2有一条正向抵达B1的路线。
同理B3可见B1、B2、C1、C2、D1、D2、E1。
强可见(strongly seeing)
当事件B能找到事件A的所有路径中跨越了绝对多数的节点,那么事件B强可见事件A。白皮书中提到经过数学论证可以保证两个强可见的节点在虚拟投票时能获得一致的结果;
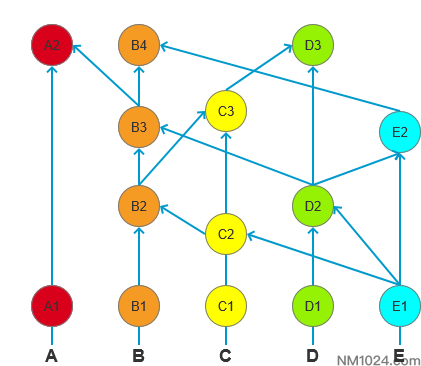
在下图中A2是可见E1的,经过的路线有[A2-B3-D2-E1],总计跨越ABDE四个节点超过绝对多数(5*2/3),即A2强可见E1。
在B4可见E1的路径中,有两条路线[B4-B3-B2-C2-E1]、[B4-B3-D2-E1]、[B4-E2-D2-E1],分别跨度BCE、BDE、BDE,独立计算的话都不够绝对多数,但多条路线合计是BCDE,是超过绝对多数的,此种也算作B4强可见E1。
见证人(witness)
每个节点在每个轮次中创建的第一个事件就是见证人事件,即该轮次的祖先事件,节点可能在某个轮次中没有见证人事件;初始节点也是见证人,在上文中的图中,A1B1C1D1E1均为初始见证人;
创建轮次(round)
轮次是属于事件的属性,根据事件所处的可见状态,把他们分为不同的轮次。一个事件的创建轮次是R或者R+1,其中R是该事件父节点的最大轮次。仅当一个事件强可见R轮次见证人事件的数量达到绝对多数时,就认为该事件在一个新的轮次上,记为R+1。(初始事件都属于第一轮次)
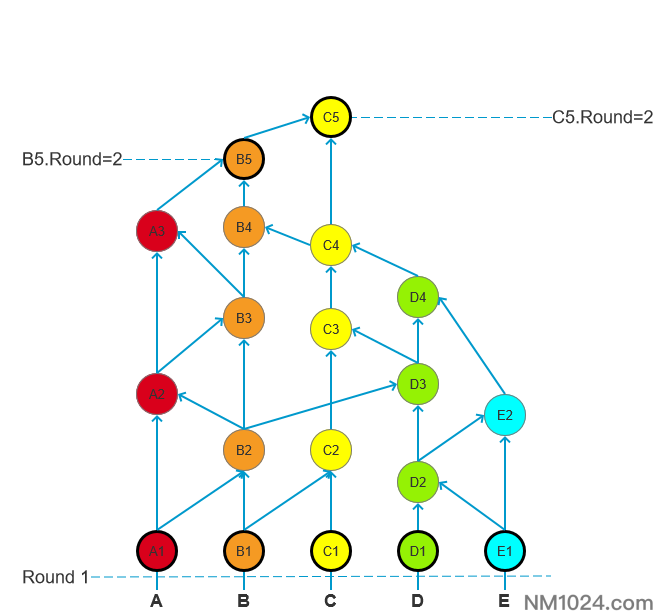
在下图中有:
B5通过[B5-B4-C4-D4-D3-B2-A1]路径,经过ABCD节点,故而强可见见证人A1;
B5通过[B5-B4-C4-D4-D3-B2-B1]、[B5-A3-A2-B2-B1]路径,经过ABCD节点,故而强可见见证人B1;
B5只有[B5-B4-C4-C3-C2-C1]到达C1,未达到绝对多数的节点数,故而无法强可见见证人C1;
B5通过[B5-B4-C4-D4-E2-D2-D1]路径,经过BCDE节点,故而强可见见证人D1;
B5通过[B5-B4-C4-D4-E2-E1]路径,经过BCDE节点,故而强可见见证人E1;
可得:B5强可见4个不同节点的见证人,超过了绝对多数,则B5为R+1轮次,并为R+1轮次的B节点见证人。
同理可推出:B5的子事件C5,延续了B5的全路径,并且C5无法强可见R+1轮次见证人事件,则C5为R+1轮次,并为R+1轮次的C节点见证人。
知名见证人(famous witness)
如果R轮的见证人能被绝对多数的R+1轮见证人可见,则它就是知名见证人,至少需要3轮才能确定一个知名见证人,某轮次的知名见证人数量不定;
在下图中:
A4可见A1,B5可见A1,C5可见A1,D5可见A1,经过的节点数达到了绝对多数,且A5、B5、C5、D5为R+1轮的见证人,故而A1为R轮的知名见证人。
同理B1、C1、D1、E1也是R轮的知名见证人。
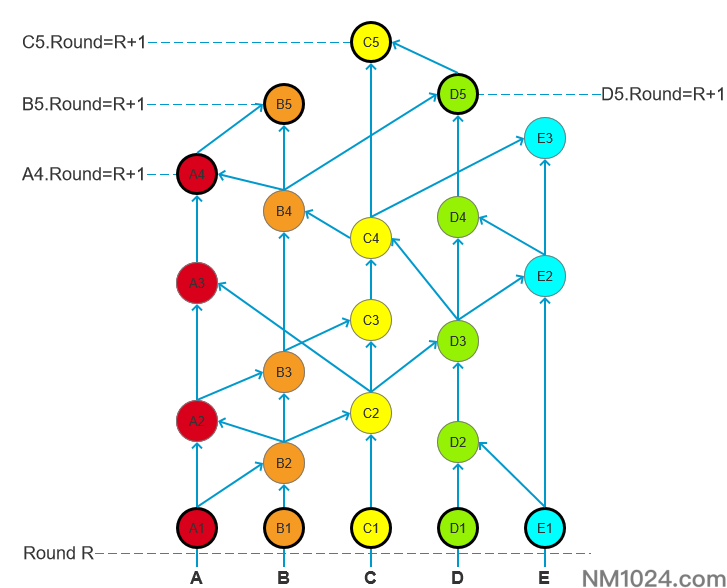
以上可以推导出A1、B1、C1、D1、E1为知名见证人,但是无法全网认证,因为节点之间并不知情:
A4、B5、C5、D5分别给A1投票表示可见,理论上A1即为知名见证人,但是C5并不知道A4与B5给A1投票了,它只看到了C5、D5的投票,所以在当前情况下A1没有被全网认证为知名见证人。
所以在见证人投票选举知名见证人之后,需要有人统计并唱票,做出决定。
接受轮次(round received)
如果R轮(创建轮次)中的所有知名见证人可见某一普通事件,则该事件的接受轮次就是R轮,如果某普通事件没有被R轮所有知名见证人可见,则它的接受轮次一定晚于R轮。
假设下图中R+1轮的四个事件已经被子孙事件确定为知名见证人。
在图中的所有黑色节点事件都有一个特点:可以同时被R+1轮所有的知名见证人可见,则认为这些黑色事件的接受轮次是R+1轮。
确认了接受轮次就意味着这些节点达成了全网共识,而共识事件的排序依据依次为:接受轮次>中位时间戳(Median timestamp)>通过算法对签名计算得出的结果。
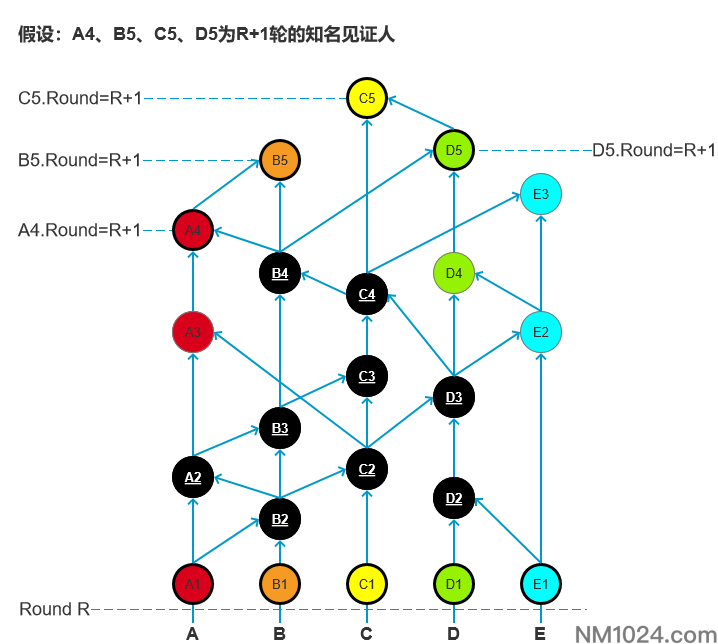
在上图中依然有部分节点在R+1轮没有被接受,这些节点将会由后续其他轮次的知名见证人接受。
中位时间戳(median timestamp)
中位时间戳是指某事件最早不同节点可见的时间戳集合。
如图中C2,最早可见C2的节点的集合是[C2,A3,B4,D3,E2],求出事件集合时间戳的中位数,认定其为C2的共识时间戳。

投票过程
- 确定R+1轮见证人;
- R+2轮见证人投票R+1轮知名见证人;
- R+3轮见证人统计的票,确定R+1轮知名见证人有效;
- R+1知名见证人确定R轮普通事件的接受轮次。
确定见证人
根据见证人的定义将每轮的见证人标记出来:
下图中所有黑色框的节点事件为见证人。总计有4个不同轮次的见证人。
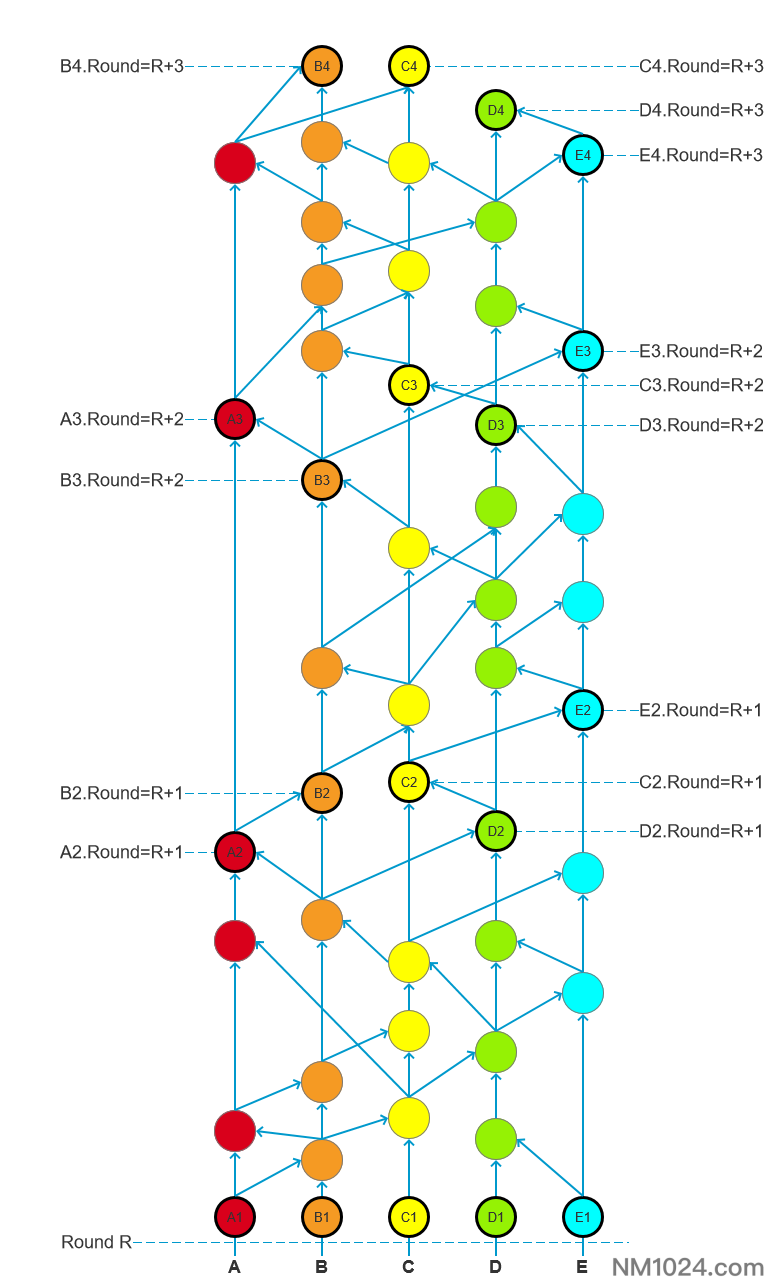
见证人投票知名见证人
由每个R+2轮的见证人投票选举出R+1轮的所有知名见证人,如下图所示:A3、B3、C3、D3、E3都可见A2,分别向A2投票YES;同理B2、C2、D2、E2也会被验证投票。
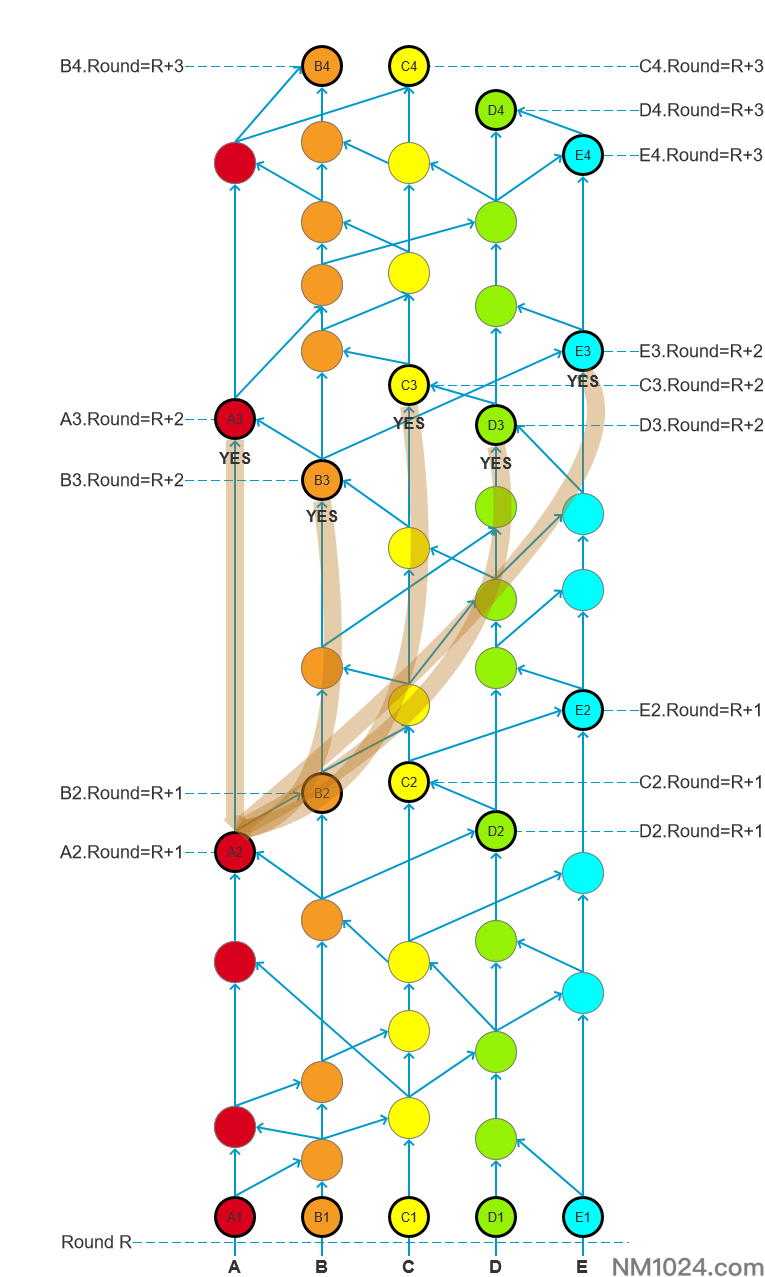
唱票选举知名见证人
再R+2轮投票完成后,将由R+3轮的见证人统计唱票:
下图中从E4事件出发强可见A3、B3、C3、D3,收集到4票关于A2是知名见证人的投票,且的票数超过绝对多数,统计完成即确认A2为知名见证人。
只需要有一个节点统计票数并且通过那么即刻达成全网认证。(白皮书有数学验证可以保证所有其他见证人也做出同样的决定)
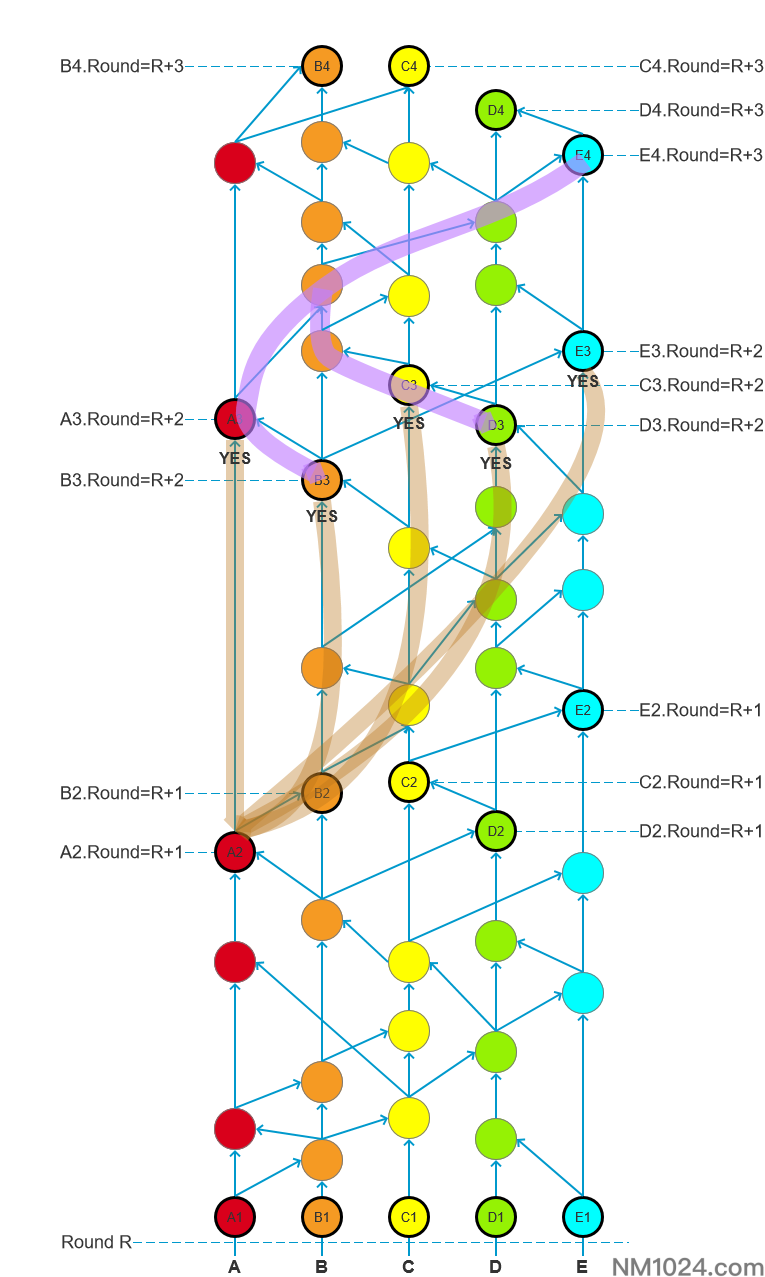
根据数学理论证明,任何一个R+2轮见证人如果统计了投票结果并做出了决定,那么这个结果就是全网的结论,如果这轮见证人无法做出决定,就由下一轮见证人计票决定,直到得出确切结论。
假如在下一轮无法做出决定,则将延续到下一轮,根据数学定理只要我们在每十轮增加一个随机轮次(coin round),则选举过程最终一定会结束(以概率1收敛)。在随机轮中,收集到绝对多数结果的见证人仅投票而不做决定,而其他见证人则根据数字签名的中间位进行随机投票。
根据以上理论可以得出A2、B2、C2、D2、E2均为知名见证人。
知名见证人确定接受轮次
将R轮能被R+1轮的知名见证人(A2、B2、C2、D2、E2)同时可见的事件标出:
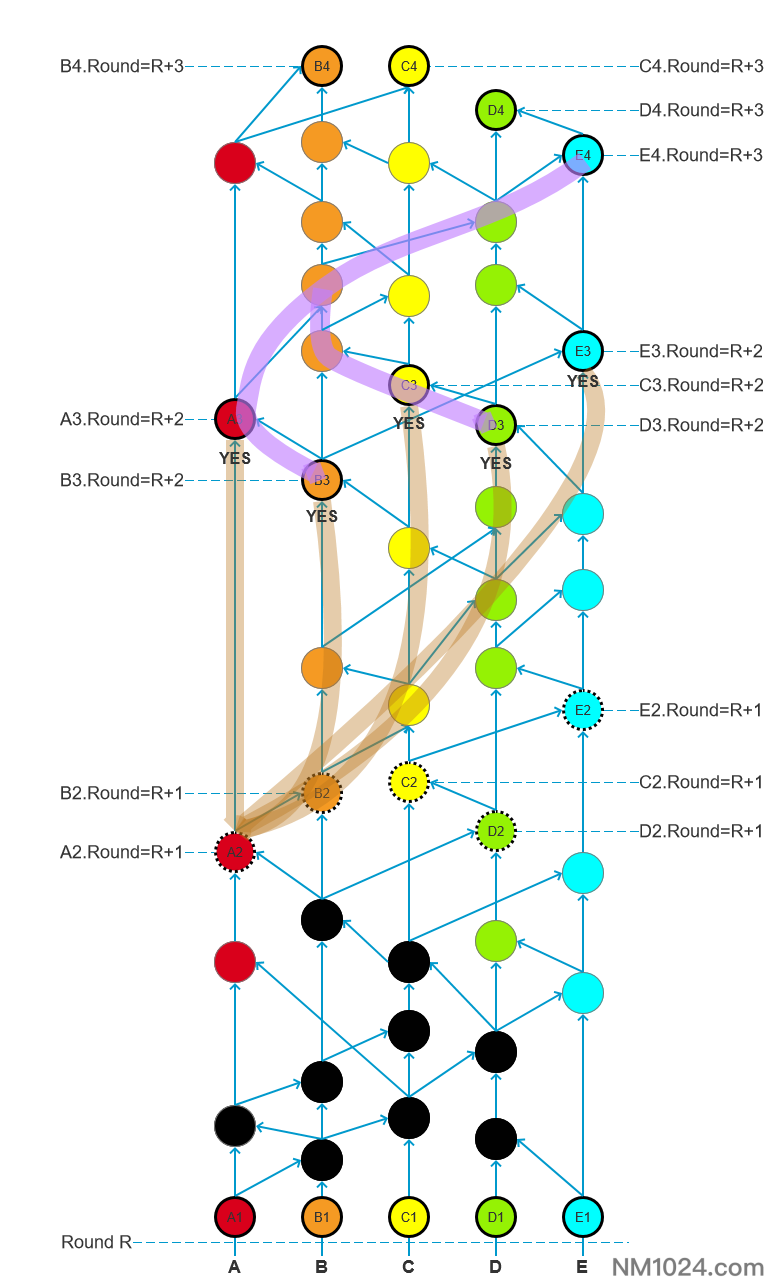
即图中在R+1轮接受的节点总计14个(加见证人),将节点按照:接受轮次>中位时间戳(Median timestamp)>通过算法对签名计算得出的结果,排序即可得到对于当前已接受事件的共识顺序。
.
.
.
.
.
.
【本文章出自NM1024.com,转载请注明作者出处。】
>>转载请注明原文链接地址:Hashgraph算法解析
